Methods: state estimation, hydrographic section analysis, and POP mode

Hydrographic section box inverse analysis

To estimate velocity based on the hydrographic data set we will use the formulation and much of the inverse software developed for the Pacific Ocean WOCE-era synthesis, designed to combine meridional and zonal sections (Macdonald et al., 2009,), and for the similar ongoing effort in the Atlantic that is designed to make greater use of the available chemistry than for the Pacific (see NSF Prior Support). The analysis differs from most other Indian Ocean inversions through incorporation of intersecting zonal and meridional lines with specific treatment of the crossovers (Johnson et al., 2001), use of full vertical resolution CTD data, and large versatility in constraints.; Transport constraints, such as those from subsurface float data, can be used, as in Wijffels et al. (2001). Air-sea fluxes can be diagnosed from the solution or used as constraints.

The proposed inverse models are defined by boxes, bound by the hydrographic lines, specified density surfaces, topography and land. The pattern of sections allows us to bound a variety of geographic regions, each with potentially differing balances of processes, all of which are part of the overall Indian overturn and mixing.  For instance, there are boxes that enclose the western boundary currents, the subtropical gyre, the equatorial region, the Indonesian outflow, the Arabian Sea, and the Bay of Bengal.  Various boxes enclose portions of the major bathymetric ridges that traverse the Indian Ocean, each of which could enhance turbulent mixing due to rough, steep topography (Becker and Sandwell, 2008), but not all with equal efficiency (Egbert and Ray, 2001; Kunze et al., 2006; Drijfhout and Naveira Garabato, 2008).

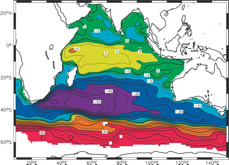
Three models will be constructed. The first uses only zonal lines (Fig. 2.1) and will be used for dual purposes of testing and comparison to the literature, and to address the first goal concerning meridional overturn.   This version will also be used for the suite of repeated sections at 32°S, partially addressing the third goal of decadal variability analysis.  Then the meridional lines will be added to create smaller boxes with one model setup for the SW monsoon and one for the NE monsoon period (Fig. 2.1 right), partially addressing the second goal of regionality and time dependence.

Using the observations, each model will be defined by a set of simultaneous linear equations that are solved using a Gauss-Markov type tapered weighted least squares (Wunsch, 1996; Ganachaud, 2003; Macdonald et al. 2003, 2009).   The ocean is divided into density layers; conservation of properties within the layers and sets of layers provides the general equations to be solved. Initially conserved are: mass top to bottom, silicate top to bottom (except in the Southern Ocean), volume in all layers, and salinity, heat, and PO (phosphate/oxygen combination 1:170) anomaly (Anderson and Sarmiento, 1994). The complete suite of chemical tracers collected on the sections, many yielding independent information (including CFCs  and carbon parameters), provides a unique opportunity for constraining the deep circulation. There is possibly enough coverage of ³He along all of the sections to make it interesting to consider as a constraint, especially in the deep layers where its source is the mantle (Srinivasan et al., 2004). Property anomaly constraints reduce the influence of noise arising from mass conservation on the property conservation constraints (Wijffels, 1993; Ganachaud, 2003).  Initial estimates of freshwater fluxes will be included, along with topographic constraints that limit the flow within constricting bathymetric features.

Many sections also have ADCP and lowered ADCP data that we will use to constrain velocity calculations (e.g. Beal and Chereskin, 2003).  There are now also two basin-wide, independent velocity analyses that can be used to constrain transports: the mean flow at 900 m from the Palace subsurface float array (Davis, 2005) and the geostrophic reference velocity solutions for each station pair in the 1995 survey from Reid (2003) (Fig. 3.1).  The Reid velocities have been used previously to estimate meridional overturning, and heat and freshwater transport (Talley et al., 2003; Talley, 2003, 2008).

Unknowns to be determined by the constraints placed on the fields include the geostrophic reference velocities, diapycnal (dianeutral) velocity and diffusivity, and layer source-sinks, including air-sea fluxes for the outcropping layers.  The knowns in the system are the relative velocity and property fields from the hydrography, along with velocity and transport estimates from the literature and estimates of uncertainty on all constraints. One source of the initial estimates of  (co)variance in the solution and the constraints will be the 0.1° POP GCM run discussed below. Air-sea exchange will be determined first as a residual calculation and secondly it will be included as an unknown source/sink term in outcropping layers and solved for by the inversion. Air-sea exchange estimates can be compared with independently observed air-sea exchanges.  E.g. for carbon, one comparison is with Takahashi’s 2008 global data base, based on pCO₂ data (http://cdiac.ornl.gov/oceans/LDEO_Underway_Database/LDEO_home.html), as well as the results of the OCMIP inter-model comparison (http://ocmip5.ipsl.jussieu.fr/OCMIP/).

As previously mentioned, to avoid issues with the strong monsoonal effects on circulation and surface fluxes in the tropical and northern Indian, we will analyze the Southwest and Northeast monsoon periods separately north of 15°S (Fig. 2.1). Neither is ideally sampled; the SW monsoon has better chemistry coverage (red dots).  However, we clearly cannot obtain full seasonal information from the hydrographic sections.  The state estimate and POP model output will be critical to the investigation of this monsoonally-forced region (e.g. as in Prasad et al., 2005, or Beal and Chereskin, 2003), yielding complete temporal coverage and hence the capability of discerning seasonal from wave-like variability, and providing a measure of uncertainty in overturn and mixing calculated from the hydrographic sections (see 3.1 and 3.3).  Altimetry data will also be used directly, as well as within the state estimate, to study the variability, especially in the tropics and northern Indian Ocean, as in Prasad et al. (2005).

Given the large tropical variability, why use hydrographic inverse solutions along sections when 4-D state estimation and very high-resolution general circulation models are available? Because the hydrographic data include all the tracer information and also direct velocity observations from top to bottom, and suffer no bias from missing or inadequate physics.  At depth, in particular, hydrography is the only observational source available for comparison to model results.

The resulting Indian Ocean solutions will yield a circulation estimate with better zonal resolution than the presently available basin-scale hydrographic analyses, which are based almost entirely on zonal, non-intersecting sections  (e.g. Macdonald, 1998; Ganachaud and Wunsch, 2002; Mikaloff Fletcher, 2006).   The inclusion of meridional lines in the Indian Ocean hydrographic model proposed here will map onto important regional differences in air-sea fluxes and forcing, e.g. between the Agulhas region and the rest of the subtropical gyre, between the Arabian Sea and Bay of Bengal, and will enclose different portions of the major mid-ocean ridges that are expected to be important in diapycnal mixing, allowing more localized estimates of vertical processes than simple large latitude bands.

In our analysis, we will place the results for the 1995 observation set in the context of longer-term interannual-to-decadal variability through comparison to ECCO/SOSE and POP.  POP has been pivotal in studying the strong effects of Rossby and Kelvin waves on the tropical Indian circulation (e.g. Prasad et al., 2005).   The Indian Ocean Dipole was active in 1995, resulting in a large deviation from normal in the western equatorial currents during the NE monsoon; the POP output clarifies the propagation of waves and linkage with changes in winds, at much shorter time scales than seasonal (Prasad and McClean, 2004).  Other climate variability that affects the Indian Ocean includes ENSO, which was in a normal

state in 1995 following an extended weak El Nino, and the Southern Annular Mode, which was also in a normal state following a year of very high index.

To date, no group has taken full advantage of this complete data set, with tracers and ADCP, to construct Indian Ocean circulation estimates and overturning budgets, including budgets for the chemistry, while recognizing seasonal variations.  The proposed hydrographic analysis addresses all three major goals (meridional, regional, seasonal and decadal aspects of Indian Ocean overturn).

State estimation (ECCO and SOSE)

State estimates are a relatively new research tool for hydrographic data analysis, with products becoming available in the last several years.  State estimates such as ECCO-GODAE are a least squares fit of an ocean model to ocean observations, including in situ profiles and surface observations of forcing, sea surface height and sea surface temperature (Wunsch and Heimbach, 2007).   The resulting estimate provides coverage in both space and time of the velocity, temperature, salinity fields, and an adjustment to the air-sea fluxes.   Hydrographic (temperature-salinity) data are acquired from a variety of sources including research cruises such as those in Fig. 2.1, XBT lines mainly on merchant ships, and, in the last several years, the Argo profiling float array.

The ECCO-GODAE product (http://www.ecco-group.org/) is continually evolving as it is extended in time and more data are incorporated.  The product we will use spans the years 1992 to present. It includes the 1995 WOCE Indian Ocean survey period of Fig. 2.1 and  the 2002 repeat section at 32°S, and will be extended to include the 2009 32°S repeat.  The ECCO-GODAE output is global, with 1° resolution in the horizontal, 23 vertical levels, and daily to monthly values.

South of 24°S, the high resolution (1/6°, 42-level) Southern Ocean State Estimate (SOSE) is available for 2005-2006 (https://journals.ametsoc.org/doi/full/10.1175/2009JPO4236.1; Mazloff, 2008; Mazloff et al., 2009), with an extension proposed through the International Polar Year and into 2009, so that it will include the new 200  32°S section.  SOSE’s initial condition and northern boundary condition are from ECCO, so its fields are the same as ECCO’s at the northern boundary.  Both ECCO and SOSE are based on the MITgcm.

We will use ECCO-GODAE in several ways, and SOSE when appropriate, that is, for the 2009 32°S section.  We will compute overturn and mixing in parallel with the inverse model and compare the results at the times of the synoptic sections, to begin to understand the advantages and limitations of the two  products.  We will analyze time series from ECCO-GODAE along the sections to begin to develop a context for the synoptic results. Depending on the specific region of focus, for instance the western boundary, or equator, or Arabian Sea, etc., we will look at three-dimensional fields and analyze the overturns, including time dependent terms.  Finally, we will consider using averaged ECCO-GODAE fields within the inverse model in order to extend it to the equator, similarly to the use of averaged time series of near-equatorial velocity observations used in the Pacific inverse (Macdonald et al., 2009).

The current SOSE estimate of Indian Ocean overturn in SOSE, of 5.5 Sv, is lower than most other estimates, and might be related to the assumed strength of the ITF in ECCO (Mazloff et al., 2009).  Comparison with details of overturning as diagnosed from the synoptic sections might assist in understanding issues with the state estimate.

POP model

The WOCE-era eddying (0.1°42-level) global configuration of the Los Alamos National Laboratory (LANL) Parallel Ocean Program (POP) simulation will be used to complement the inverse calculation and the state estimation in understanding the IO overturn. It will provide a space-time context with a largely-resolved mesoscale for the interpretation of results from these other calculations. Information from POP is expected to be especially essential in the tropical and northern Indian Ocean where the circulation is strongly seasonal and the observational coverage in each season is incomplete.  POP will also provide the opportunity to study the dynamics of some of the processes that might be important for the overturn and mixing, particularly resulting from adjustment to changing forcing in the tropics.  ECCO, with 1° resolution, is likely to be too coarse to be ideal for this purpose.

The fidelity of the model output will first be determined by comparing it with ancillary data such as altimetry particularly in the context of intraseasonal and monsoonal variability. The zonally-averaged meridional overturning circulation (MOC) together with overturning, gyre and eddy components of heat transport will be calculated during the two phases of the monsoon and on annual time scales to the north of the Indonesian Throughflow. Also these quantities will be calculated for years depicting the two phases of the Indian Ocean Dipole Model (IOD). The relative importance of zonally and vertically integrated meridional heat transport divergence, net heat flux, rate of change of heat content, and lateral diffusive flux divergence at a given latitude in the northern Indian Ocean will be calculated on a monthly basis over the period of the integration. Heat and salt budgets will be constructed for the Arabian Sea and Bay of Bengal for the monsoon periods, annually, and for years associated with the two phases of the IOD. As such, we will obtain an understanding of the overturn associated with each of these basins. Ventilation processes in POP can be examined using ideal age, which provides a measure of the time since a water parcel was last in the surface mixed layer, in contact with the atmosphere. We can calculate the volume of water with mean age of the time scales of interest in these two basins to further understand overturn variability.

POP has been configured on a tripole grid, which is Mercator up to 28.5°N. As well, partial bottom cells (PBC) have been used in this simulation; PBCs (Pacanowski and Gnanadesikan, 1998) improve the presentation of the flows over the ocean floor. The simulation has been run for 104 years; as such, it is the first centennial ocean simulation conducted at such fine resolution. It is forced with the monthly normal year atmospheric fluxes constructed by Large and Yeager (2004) for the Common Ocean-Ice Reference Experiments (CORE). Normal year forcing consists of single annual cycles of all atmospheric data needed to force an ocean model and is representative of climatological conditions over 43 years of interannually varying atmospheric state. The forcing uses the NCEP/NCAR reanalysis corrected with scatterometer data that in particular improves the representation of the tropical circulation. A marked improvement was seen in the representation of the Northwest Corner in the North Atlantic and the pathways of the Agulhas eddies, relative to the global 0.1°, 40-level standard z-level dipole simulation of Maltrud and McClean (2005). Sensitivity studies showed that the PBCs were largely responsible for these improvements (Maltrud et al., 2008). A review of the fidelity of the spun-up ocean state was presented by Bryan (NCAR) at the CCSM Ocean Modeling Working Group in December 2009.

It is proposed here to conduct a 5-year global tripole 0.1° POP simulation forced with interannually-varying synoptic CORE forcing for the years 1994-2000 initialized from this spun-up ocean state; the simulation will be continued through 2006 using resources from another funded grant (Kuroshio Extension) and output from these years will also be available for the proposed Indian Ocean study. These years coincide with the WOCE data collection years and the 2002 32°S and 2003 20°S repeat sections. As well as property transports across WOCE sections in the Indian Ocean, both state variables and cross-terms for flux calculations will be archived on a high-frequency basis (daily) to permit consistent comparisons with the data collected during the field experiment years. One may argue for the use of a regional Indian Ocean model in this study, however, given the key thermohaline linkages between the Indian Ocean and adjacent basins, the availability of the global grid and initial condition, the additional cost that would be associated with reconfiguring a regional model, and McClean’s experience with global POP, it is reasonable to proceed as proposed. Additionally, both F. Bryan (NCAR) and M. Maltrud (LANL) have provided letters of support for this project. CFCs will be included in the run for the benefit of their research, hence they will bring their expertise to bear on the execution of this simulation.