Entropy and Scintillation Analysis of Acoustical Beam Propagation through Ocean Internal Waves
Collaborators: Andrey K. Morozov, John A. Colosi
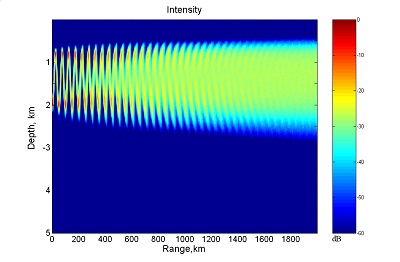 Parabolic equation numerical simulations of waveguide acoustical beam propagation in an ocean of Garrett-Munk internal waves are used to examine the range evolution of beam properties such as beam width (both spectral and spatial), Shannon entropy, and scintillation index, as a function of beam angle. The ray trajectories associated with these beams are predominantly chaotic or exponentially sensitive to initial conditions and/or medium perturbations. At long range near saturation the finite frequency beams show a constant rate of change of Shannon entropy with range, independent of acoustic frequency. This full-wave rate of entropy is of the same order of magnitude as the average rate of entropy for the ray trajectories associated with this beam. Finite range Lyapunov exponents, provide the estimates of ray entropy rate or Kolmogorov-Siani entropy. The correspondence between full-wave and ray entropies suggests a full-wave manifestation of ray chaos, but only once statistical saturation is obtained. In spite of this correspondence, the simulated acoustical beams expand diffusively not exponentially (or explosively).
Parabolic equation numerical simulations of waveguide acoustical beam propagation in an ocean of Garrett-Munk internal waves are used to examine the range evolution of beam properties such as beam width (both spectral and spatial), Shannon entropy, and scintillation index, as a function of beam angle. The ray trajectories associated with these beams are predominantly chaotic or exponentially sensitive to initial conditions and/or medium perturbations. At long range near saturation the finite frequency beams show a constant rate of change of Shannon entropy with range, independent of acoustic frequency. This full-wave rate of entropy is of the same order of magnitude as the average rate of entropy for the ray trajectories associated with this beam. Finite range Lyapunov exponents, provide the estimates of ray entropy rate or Kolmogorov-Siani entropy. The correspondence between full-wave and ray entropies suggests a full-wave manifestation of ray chaos, but only once statistical saturation is obtained. In spite of this correspondence, the simulated acoustical beams expand diffusively not exponentially (or explosively).
1. Morozov A.K., Colosi J.A. Entropy and scintillation analysis of acoustical beam propagation through ocean internal waves. JASA, 117(3), Pt. 2 March 2005, pp. 1611-1623.
2. Morozov A. K. Colosi J. A., Stochastic Differential Equation Analysis for Sound Scattering by Random Internal Waves in the Ocean, Acoustical Physics, 2007, Vol. 53, No. 3, pp. 335-347.
3. Colosi J.A., Morozov A.K. Statistics of normal mode amplitudes in an ocean with random sound-speed perturbations: Cross-mode coherence and mean intensity, J. Acoust. Soc. Am. 126 Issue 3, 1026-1035 (2009).
Funding Agency
