Boundary Mixing
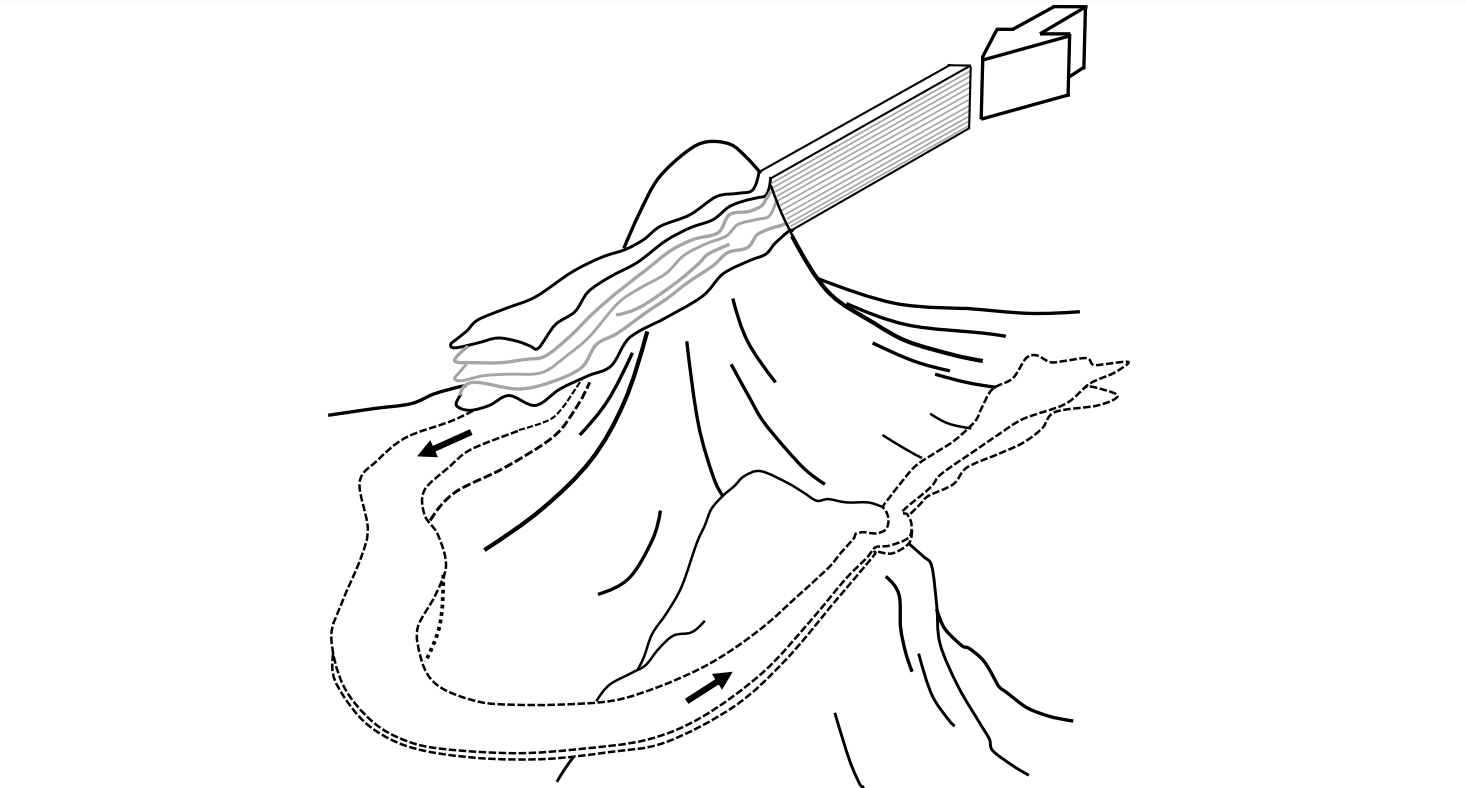
I like to start talking about boundary mixing by referring to a ‘discussion’ between Larry Armi and Chris Garrett that appeared in in JGR during 1979, with two associated figures. Larry was interpreting temperature and density traces from CTD data as boundary layers and boundary layer separation processes. Chris, coauthor of the celebrated Garrett and Munk series, makes some rather pointed remarks and, in the process of doing so, draws a picture of a boundary layer over sloping topography.
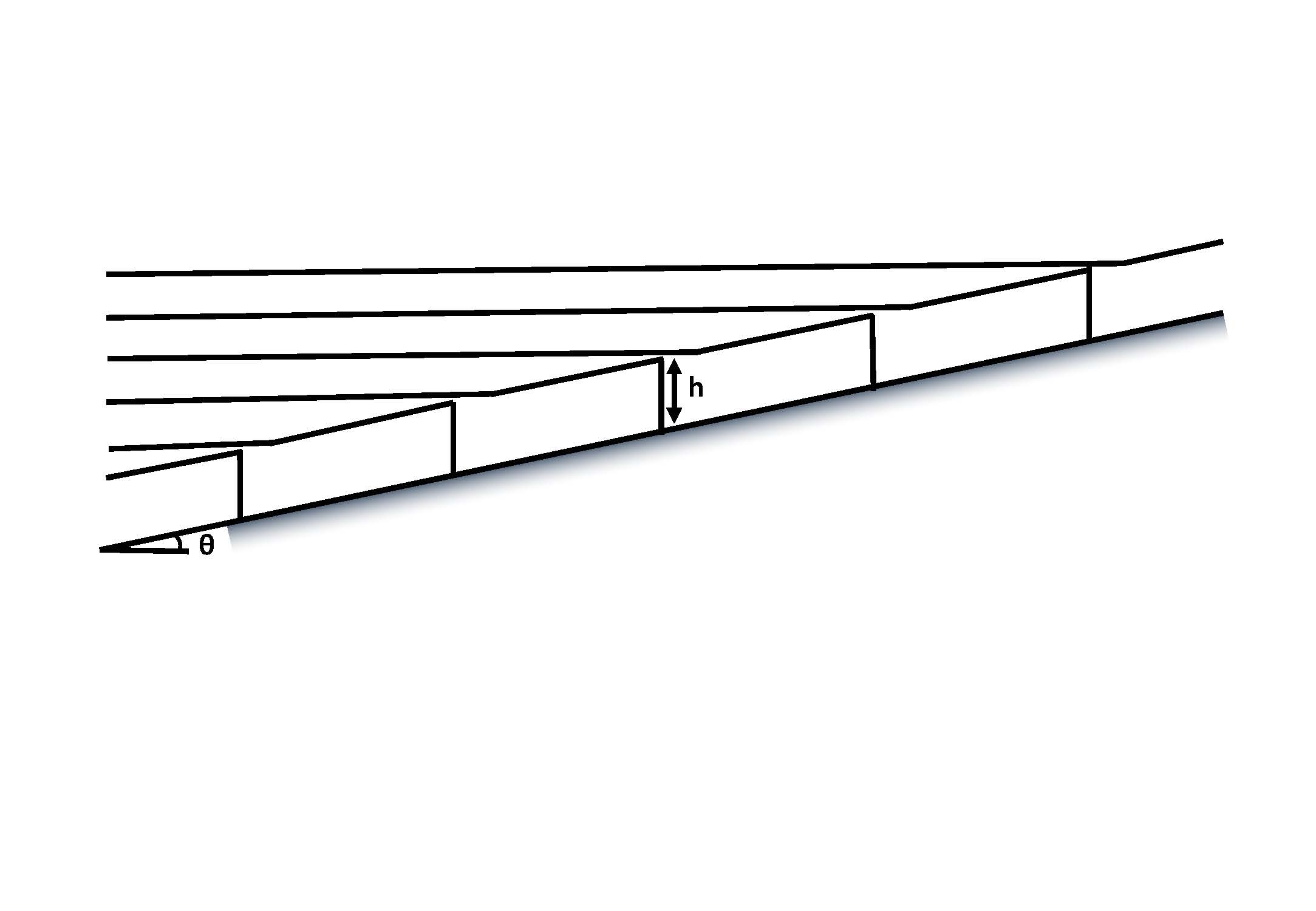
That figure is presented as if everybody knows that this is what the ocean's bottom boundary layer should look like, and, starting with Phillips 1970 and Wunsch 1970, in the fullness of time that theory evolves what I refer to as the 'one-dimensional model'. This 'one-dimensional model' is the subject of a chapter with Trevor, to which I refer you to for the details. The short version is that this model has many assumptions:
| Assumptions | |
|---|---|
| Subinertial .............................................. | •Discards coupling of BBL with IW field |
| Isotropic mixing .................................. | •Not true for Internal waves |
| Flux-gradient relation for buoyancy ................................................. | •Not true for Convection |
| No-normal flux bbc dominates .............................................. |
•BBC for viscous and form drag dominate |
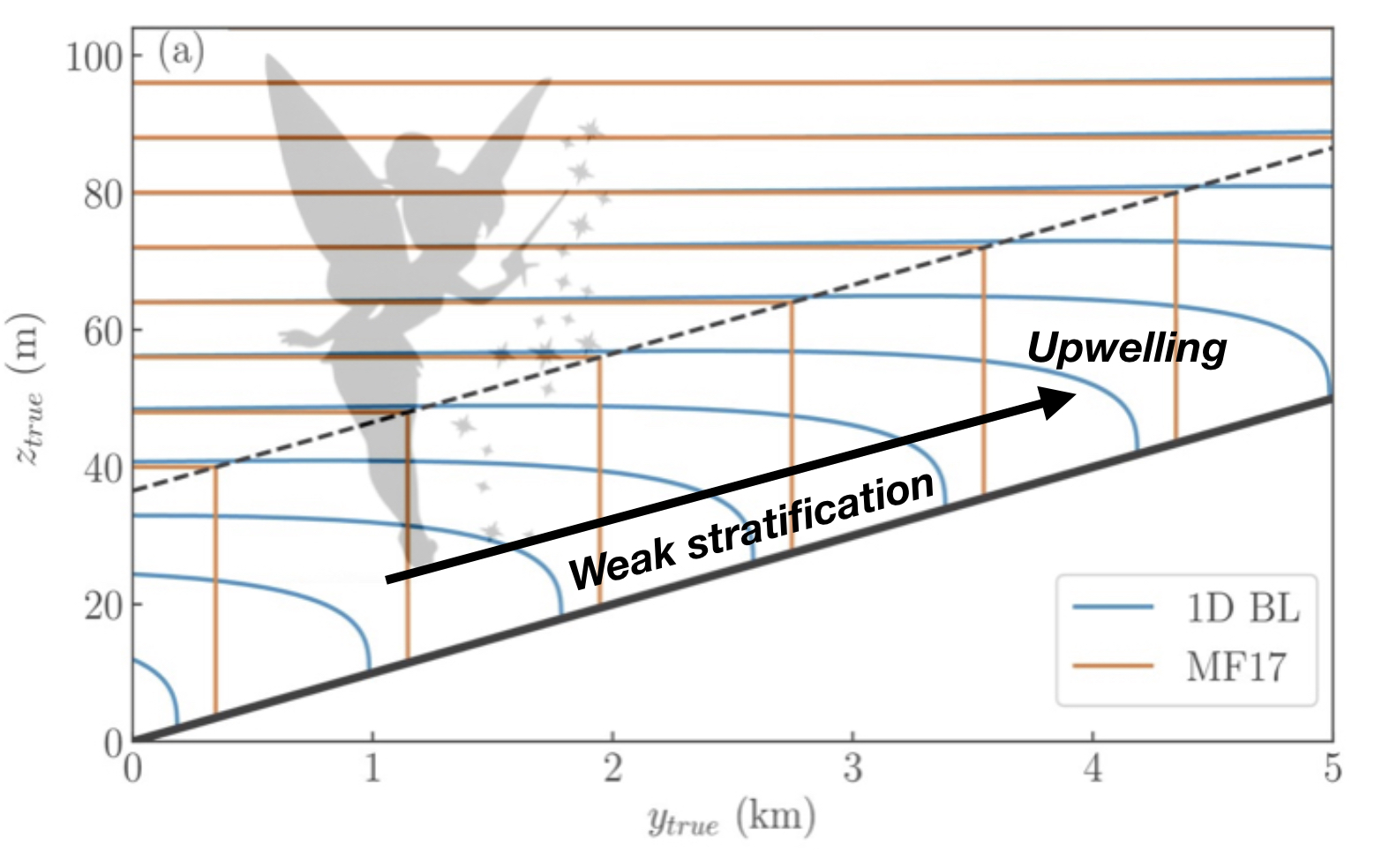
none of which are particularly true for internal waves due to issues on the right. The core of the one-dimensional model is to sprinkle some mixing on a slope and ask how it adjusts. The one dimensional model, captured in the figure below, provides expectations of a buoyancy anomaly at the slope with upwelling located there.
What I am trying to accomplish in the chapter is to emphasize the potential for differential advection of buoyancy initiated by drag to result in convection. Implied is a direct coupling of the internal wavefield with the bottom boundary layer. A generic label for this behavior is 'Internal Swash".
The one dimensional model emphasizes the importance of the no-flux boundary condition on buoyancy and drag is just something that tags along on the residual flow. My effort has been to promote drag as a more important boundary condition as it dictates the phenomenology of the mixing process.
There is significant data coming online from DYNOPO (Naveira Garabato 2019, Spingys et al. 202Polzin et al. 2022), GoMIX (Polzin et al. 2021, plus drafts) and BLT that will inform on this matter, complementing work from BBTRE and TWIST that remains to be published.
There are many projects here involving both bottom boundary layer dynamics, tidal energetics and control volume studies.