Wave Dynamics
Polzin and Lvov 2011 RoG was a labor of love. It documents the regional variations in internal wave spectra and then lays out possible reasons for that variability: sources, sinks and spectral transfer mechanisms. A summary figure from that study appears to the right.
I. Wave-wave interactions
A. Practical Tools for downscale transport
Finestructure parameterizations, or how to parameterize internal wave dissipation using instrumentation that does not have access to the proper scales. See Polzin et al. 2014 JGR for a review. It will take you through Polzin 2004a JPO and Polzin et al. 1995 JPO.
Richardson Number / shear instability closures: Polzin 1996 JPO.
This is a story about how the downscale transport from internal waves is handed off to turbulence via a wave breaking (shear instability) process.
B. PSI decay of internal tides through weakly nonlinear interactions.
The algebra appears in Polzin and Lvov 2011 RoG. There are incipient projects using data from NATRE and BBTRE about how draining energy from the internal tide to the near-inertial and then to high frequencies accounts for the regional internal wave spectrum.
C. Theoretical approaches to internal wave interactions
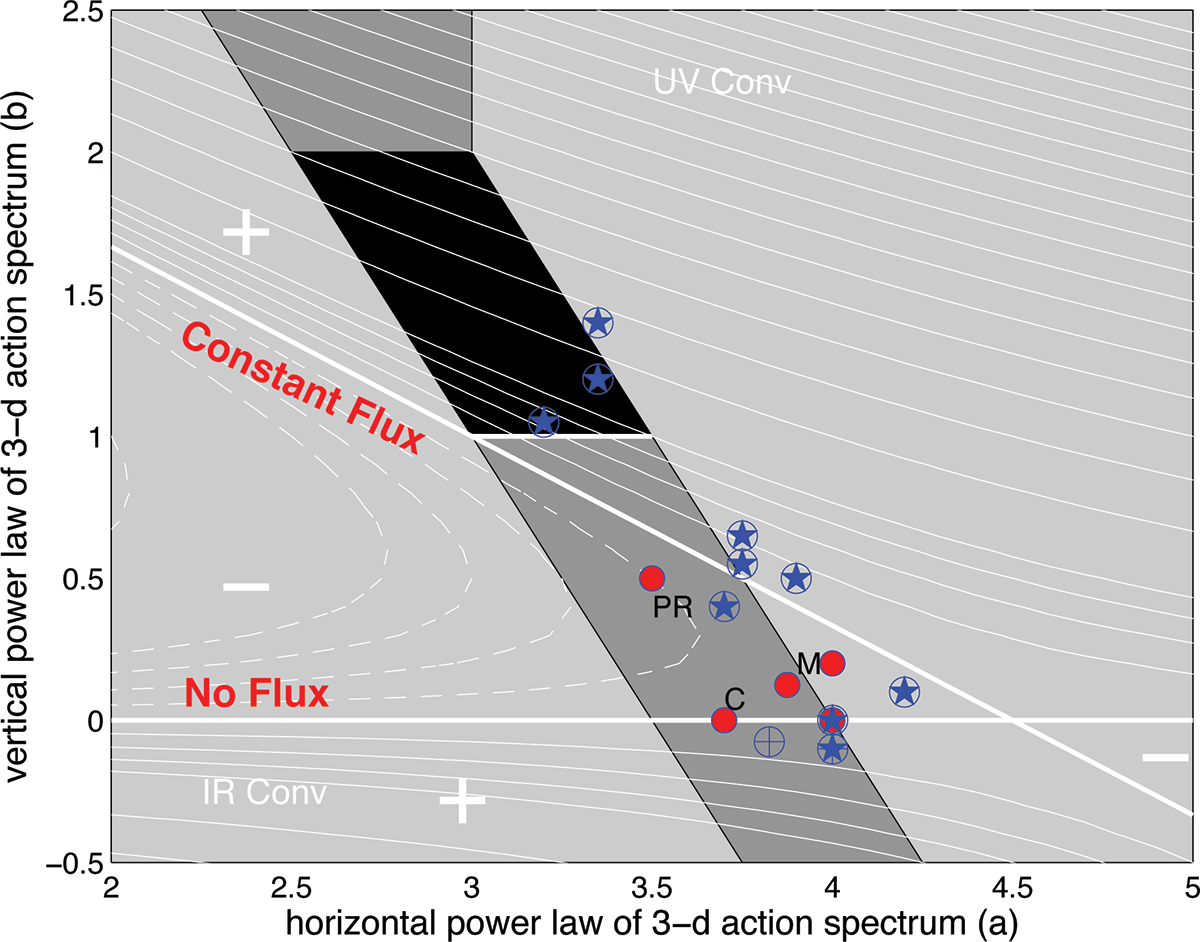
The difference between theoretical predictions and what is required by our observational knowledge of sources and sinks (see nearly anything I've written on waves) is such that we (Polzin and Lvov 2017 Fluids, Dematteis et al. 2022 JPO) refer to this growing set of contradictions as the ’Oceanic Ultraviolet Catastrophe’. The key realization is that singularities in the kinetic equation (Lvov et al. 2010 JPO) are highly problematic and that singularities in vertical wavenumber are the ones that dictate possible solutions, with interactions in horizontal wavenumber locating a particular stationary state - Dematteis et al. 2022. This information is in the power law - power law scatter plot at the top. Giovanni Dematteis deconstructs interactions into 'local' and 'extreme scale separated', with 'local' interactions in remarkable agreement
with the finescale parameterization. These local interactions appear to be unhinged from the dominance of the singularities in vertical wavenumber, which Yuri and I are singling out (Polzin and Lvov 2017, two nearly submitted papers) for study. In order to understand this we needed to reject the fourth order cumulant hypothesis that underpins the kinetic equation and are reaching into literature on open quantum systems to discuss why action spectral density is NOT conserved following ray trajectories. Talk to me for details.
D. Wave-mean flow interactions
There are three stories here, all originating from work done in the 70’s and sparked by a figure in Buehler and McIntyre (2005). On an intellectual level, this insight lets you transcend the limitations of a near-inertial dispersion relation appearing in Kunze (1986) and Young and Ben Jaloul (1999) in which advection is regarded as a small parameter. In contrast, when you have sufficient data to define a 3-d wave vector associated with coherent finescale features, one finds that advection is O(1).
At stake are fundamental conservation principles of momentum and potential vorticity.
The first (Polzin 2008 JPO) is a story about critical layers in 3-dimensions rather than 2 using Tom Sanford’s original Mode EMVP data. An important finding is that advection plays an important role. More examples are catalogued in Meyer et al. (2015). See also Waterman's (2021) life cycle story. Amelie's analysis needs to be ported through Stephanie's take. What you will find is that coherent packets caught up in critical layer events originate at the surface as waves with intrinsic frequencies of twice f.
The second is a story about energy and momentum/potential vorticity exchanges between internal waves and mesoscale eddies using data from the PolyMode Local Dynamics Experiment. Correlations between wave stresses and eddy rates of strain are used to define effective viscosity operators. See also Cusack et al. 2020.
The third is a revisit of P. Muller’s dissertation to develop a
diagnostic model for the stress-strain relations. I was stunned by this as I always thought eddy viscosity was a notion you employed to disguise your ignorance. Peter was disturbed by my take and sent the manuscript back to me without review. I think Peter got stuck in a paradigm based upon amplitude modulated waves in a kinetic equation with a PV constraint and couldn't see the link between frequency modulated waves (wave packets), PV anomalies on the packet scale and extreme scale separated wave-wave interactions. Talk to me if interested.
E. Coupling Surface Gravity waves and Internal Gravity waves.
There are important implications here concerning upper ocean mixing. These are motivated by observations reported in Forryan et al. 2015 concerning the rapid injection of near-inertial shear into the upper ocean. There are parallels to the October Storm (Ocean Storms literature) that suggest a near-instantaneous injection of momentum into the ocean by a wave process. Talk to me.
Projects:
a) investigate PSI with NATRE and BBTRE data sets
b) revisit the RoG with the intent of looking at boundary processes rather than the interior wavefield in the farfield of possible sources.
c) developing prognostic models to predict the internal wave spectrum from source-sink distributions