The womb of nature and perhaps her grave

Entropy is a squirrely concept that strains the patience of many a student taking a physical chemistry course. Mathematically abstract and conceptually weird (for lack of a better adjective), entropy is something I have to reread the basics on every time I stumble across it. Wrapping my mind around entropy often ends with me shoving away my old Thermodynamics notebook and letting my head fall on my desk in despair. Why would one bother?

We bother because entropy is central to our understanding of whether or not basic physical processes and chemical reactions that we care about will occur. The Second Law of Thermodynamics tells us that, unlike the energy of the universe, which always stays the same, entropy is a property that always increases. A tendency towards greater entropy explains why ice melts, water evaporates, wood burns, and a drop of red wine added to a swimming pool quickly diffuses throughout the whole pool rather than staying bunched up in a little clump of color.

So, what is entropy? You may have heard entropy described colloquially as a measure of disorder. A well-organized bedroom with the bed neatly made and books lined up alphabetically on their shelves would be a low-entropy system, whereas a room with books, blankets, and clothes strewn in chaos around the floor would be high-entropy system. This conceptualization of entropy can be used to explain why ice melts or water vaporizes, at least if there is enough heat available: Ice has a highly ordered crystal structure, whereas liquid water has molecules that more loosely ordered and disorganized, and gaseous water vapor is the least structured and most disordered form of water.

Entropy and wasted energy

This “messy room” explanation, however, does not capture some important characteristics of entropy. The first of these characteristics is entropy as a measure of “useless” energy. By “useless” energy, we mean energy that is lost to the surrounding environment in the form of heat rather than energy that does useful work for us, like keeping a car engine running, or turning on a lightbulb. As we know from every day experience, car engines and light bulbs get hot—this is because they do not work perfectly efficiently, but waste some energy in the form of heat. One of the mathematical definitions of entropy is written in terms of this heat loss. The Claussius inequality for the entropy change that a real-world process (an “irreversible” process) contributes to our system (by “system,” I mean our lightbulb or car engine, or whatever else we’re interested in) is

dS > dq_rev/T

where dS is the incremental change in entropy, dq_rev is the amount heat exchanged between our lightbulb and the surrounding room for an idealized, maximally efficient “reversible” process, and T is the temperature of the room.

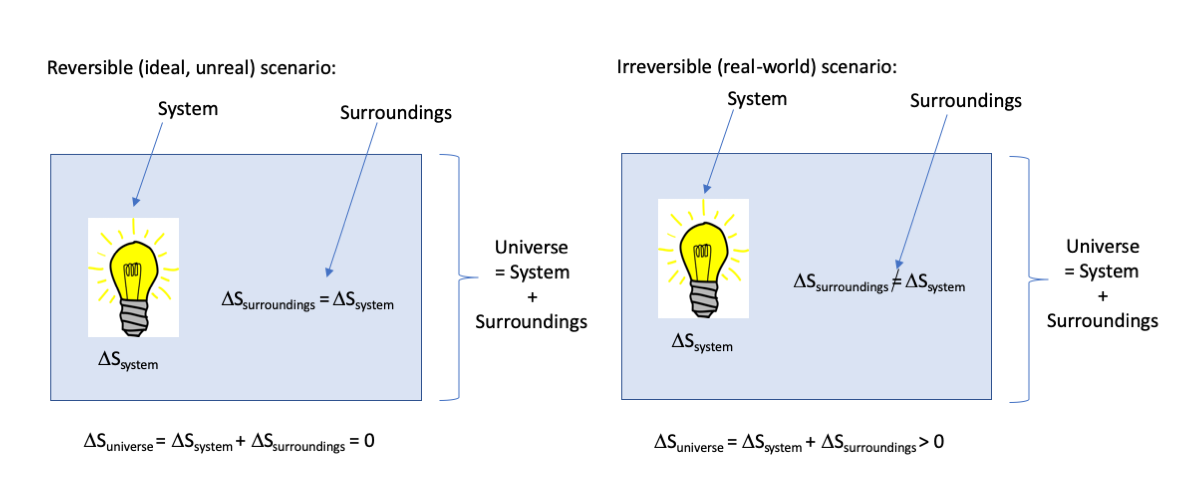
Without getting too deep into the math (a rabbit hole from which it is difficult to return unscathed), the important things to understand from this definition are (1) Entropy is defined in terms of heat loss, which we typically consider wasted energy, and (2) The entropy change for a real-world process will always be greater than the entropy for an idealized reversible process. An important note is that this inequality applies only to the entropy change of our system, but to find out what the total effect of our lightbulb on the entropy of the whole universe is, we have to consider the entropy change of the environment all around our lightbulb as well (the “surroundings”). For an idealized reversible process, the entropy change dq_rev/T of the ideal lightbulb is perfectly counterbalanced by the entropy change of the surroundings, resulting in a net change for the universe of zero. For any real, irreversible process, however, the entropy changes for the lightbulb and the surroundings are slightly out of balance and always results in a net increase of entropy for the entire universe. This is the Second Law of Thermodynamics:

For a reversible process,

ΔS_universe = ΔS_system + ΔS_surroundings = 0

And for a real-world irreversible process,

ΔS_universe = ΔS_system + ΔS_surroundings > 0

There’s no going back! Literally everything that happens in the entire universe results in the dissipation of wasted energy and an increase in entropy. The house always wins; us puny humans with our inefficient machines can’t even break even.

Entropy and equilibrium

The second characteristic of entropy I want to share is entropy as a measure of homogeneity, or sameness, in a system. I find that this aspect of entropy is truly not captured in the “messy room” analogy. When I think of a messy room, I think of a good deal of heterogeneity, with books and blankets and clothes all thrown about. This is not, however, what entropy is about. One of the other mathematical definitions of entropy is the Boltzmann equation:

S = k_bln(W)

Where k_b is a constant, ln is the natural log function, and W, crudely, is the number of different ways that the component molecules of a system can be arranged to result in the same energy. This definition is quite abstract. The significance of it, however, is as follows: A system contains higher entropy if there are more ways that you can arrange its component particles to get the same result. For example, if you add a drop of red wine to a swimming pool, there are very few ways that you can arrange all of the water molecules and wine molecules in the entire pool to result in a concentrated dollop of color that remains in stasis near the edge of the pool. This scenario would be a low entropy system. However, if the food coloring molecules diffuse through the pool and distribute themselves somewhat evenly, there are lots of ways you could rearrange the molecules in the pool and still end up with a system that looks pretty much the same: a pool full of water with a little bit of color spread out everywhere. This would be a high entropy system. I find this counterintuitive based on the messy room analogy, as a homogeneously-colored pool doesn’t look “messy.”

The constant increase of entropy required by the Second Law, then, would have a leveling effect: Things don’t just fall apart and get messy; they also become mixed up in their surroundings such that we lose difference. Gradients of pressure, potential energy, temperature, and so forth, all tend to wear down and achieve a state of equilibrium. In this state of equilibrium, there is no longer any driving force requiring stuff to happen.

The full weight of this idea may not be immediately apparent. The world we see around us requires gradients of difference in order to continue: Our cells generate and store energy by maintaining a proton gradient across a membrane, our oceans require gradients of density to drive their circulation, our weather patterns require gradients of temperature. The Second Law tells us that the drive towards higher entropy and equilibrium is the reason why these gradients make our world work, rather than just remaining in a state of perpetual and static difference. The Second Law also tells us that we don’t want to be around when those gradients are exhausted, like a rubber band losing its elasticity. As one of my chemistry teachers once explained, “Equilibrium is death.” Yes, this is rather pessimistic.

Paradise Lost

I am reminded of a passage from John Milton’s epic poem Paradise Lost, which describes Satan standing at the brink of the abyss before his descent into hell:

             Into this wild abyss,

            The womb of nature and perhaps her grave,

            Of neither sea, nor shore, nor air, nor fire,

            But all these in their pregnant causes mixed

            Confusedly, and which thus must ever fight,

            Unless the almighty maker them ordain

            His dark materials to create more worlds

Milton and I do not share similar world views in most respects: I would not describe my conception of heaven as a monarchy or of hell as democracy, for instance. Milton’s writing does not advocate for independent thought, learning, or scientific inquiry. But I guess one can’t expect much from a man who taught his daughters the sounds and spelling of Latin, so they could take dictation, while withholding the meaning of the words.

This writing, however, is truly beautiful. Milton wrote in the 1600s, but when I read this passage, I think of the universe starting with the Big Bang, of that pinhead containing the primordial ingredients with the potential to create well, everything. In Milton’s vision, God snaps his fingers to separate the elemental constituents of the universe “in their pregnant causes mixed” and create the difference required to drive the winds, oceans, and engines of a world. Milton also imagines the possibility that the universe could someday return to a state of high-entropy goo: His abyss contains not only “the womb of nature,” but also “perhaps her grave.” This description is clearly lyrical, unscientific, and written before the word “entropy” even existed. I value it not because it gives a didactic explanation of entropy but because it rhymes, unconsciously, with my scientific understanding of entropy. The Second Law of Thermodynamics is, as explained above, a bit scary and sad because it does indeed contain the grave of nature. Milton’s poetry takes the edge of our impending doom because it does what all good literature does, and makes even an unpleasant truth shockingly beautiful.

Most of the time, I don’t think about the philosophical connotations of the Second Law. Like most chemists, I use entropy as a tool to understand whether a reaction will be spontaneous. In everyday life, this is what entropy is useful for: determining whether a certain reaction pathway is likely to occur under certain environmental conditions. Reactions that do not increase in the entropy of the universe won’t happen and can be discarded as processes affecting our chemical of interest. I’m glad, though, that I have access to the actual meaning of entropy, which enriches my understanding of how the world works, and why.

References:

This post draws from my notes from the following courses:

Physical Chemistry I, taught by Kana Takematsu at Bowdoin College in the Fall of 2016

Aquatic Chemistry, taught by Desiree Plata at MIT in the Fall of 2019

I have not read a textbook description of entropy that I have found particularly satisfying. However, I do like the explanation given in The Cartoon Guide to Chemistry, by Larry Gonick and Craig Criddle.