Radiative Heat Fluxes

Radiative fluxes are defined with the sign convention that an upward directed flux is a positive quantity.

The prescription of shortwave radiation follows that of Parkinson and Washington (1979) and Zillman (1972).

For the ocean surface, the net downward shortwave radiation (W/m²) is modeled as

For the ice (snow) surface, the net downward shortwave radiation (W/m²) is modeled in an analogous manner as

The amount of shortwave radiation, prior to its modification by cloud cover and surface albedo effects as formulated above, is the Zillman relation

where  is the solar zenith angle, whose cosine is calculated by the geometric formula

is the solar constant, and

 is the vapor pressure of water in air.

In the above formula for shortwave radiation,

is the geographic latitude, and

 is the declination as determined by

where

is the day-of-year, expressed in 365-day format.

Care has to be taken for solar zenith angles outside the range

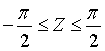that the solar radiation is set to zero

(i.e., the sun is below the local horizon in such cases).

Finally,  is the hour angle given by

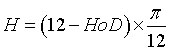
where

is the hour-of-day, expressed in 24-hour format.

The above parameterization of shortwave radiation explicitly accounts for the diurnal cycle of radiation. Models with time steps in excess of 1 hour or so are to be careful that their representation of shortwave radiation is meaningful. A suggestion for such models is to simply eliminate any attempt at resolving the diurnal cycle by instead taking the daily averaged shortwave radiation.

All angles in the above formulae are expressed in radians.

Longwave

For the ocean surface, the net upward longwave radiation (W/m²) is modeled (Rosati and Miyakoda, 1988)

For the ice (snow) surface, the net upward longwave radiation (W/m²) is modeled in an analogous manner as

NOTE: All temperatures involved in longwave calculations are in Kelvin.